求斐波那契数列(Fibonacci Numbers)算法居然有9种，你知道几种？

欢迎大家来到IT世界,在知识的湖畔探索吧!

By LongLuo

斐波那契数列(Fibonacci sequence)，又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：

欢迎大家来到IT世界,在知识的湖畔探索吧!

这个数列从第3项开始，每一项都等于前两项之和。

斐波那契数的边界条件是和。当时，每一项的和都等于前两项的和，因此有如下递推关系：

算法一: 递归(recursion)

显而易见斐波那契数列存在递归关系，很容易想到使用递归方法来求解：

public class Solution { public static int fib(int n) { if (n <= 1) { return n; } return fib(n - 1) + fib(n - 2); } public static void main(String[] args) { System.out.println("1 ?= " + fib(1)); System.out.println("1 ?= " + fib(2)); System.out.println("2 ?= " + fib(3)); } }

欢迎大家来到IT世界,在知识的湖畔探索吧!

复杂度分析：

时间复杂度：，可见是指数级的。

我们可以写出其实现
递归树，如下所示：

欢迎大家来到IT世界,在知识的湖畔探索吧! fib(5) / \ fib(4) fib(3) / \ / \ fib(3) fib(2) fib(2) fib(1) / \ / \ / \ fib(2) fib(1) fib(1) fib(0) fib(1) fib(0) / \ fib(1) fib(0) 

可以看出其做了很多重复性的计算，因此对于数值比较大时，其性能是灾难性的。

空间复杂度：，函数递归栈。

算法二: 动态规划(dynamic programming)

因为斐波那契数列存在递推关系，因为也可以使用动态规划来实现。动态规划的状态转移方程即为上述递推关系，边界条件为和。

class Solution { public static int fib(int n) { /* Declare an array to store Fibonacci numbers. */ int f[] = new int[n + 2]; // 1 extra to handle case, n = 0 int i; /* 0th and 1st number of the series are 0 and 1*/ f[0] = 0; f[1] = 1; for (i = 2; i <= n; i++) { /* Add the previous 2 numbers in the series and store it */ f[i] = f[i - 1] + f[i - 2]; } return f[n]; } } 

复杂度分析：

时间复杂度：。
空间复杂度：
。

算法三：记录值的动态规划实现

针对算法二，我们可以将计算好的值存储起来以避免重复运算，如下所示：

欢迎大家来到IT世界,在知识的湖畔探索吧! // Initialize array of dp public static int[] dp = new int[10]; public static int fib(int n) { if (n <= 1) { return n; } // Temporary variables to store values of fib(n-1) & fib(n-2) int first, second; if (dp[n - 1] != -1) { first = dp[n - 1]; } else { first = fib(n - 1); } if (dp[n - 2] != -1) { second = dp[n - 2]; } else { second = fib(n - 2); } // Memoization return dp[n] = first + second; }

复杂度分析

时间复杂度:
空间复杂度:

算法四: 空间优化的动态规划(Space Optimized)

算法二时间复杂度和空间复杂度都是，但由于只和与有关，因此可以使用滚动数组思想把空间复杂度优化成。代码如下所示:

class Solution { public int fib(int n) { if (n < 2) { return n; } int p = 0, q = 0, r = 1; for (int i = 2; i <= n; ++i) { p = q; q = r; r = p + q; } return r; } }

复杂度分析：

时间复杂度：。
空间复杂度：
。

算法五：矩阵幂

使用矩阵快速幂的方法可以降低时间复杂度。

首先我们可以构建这样一个递推关系：

因此：

令：

因此只要我们能快速计算矩阵的次幂，就可以得到的值。如果直接求取，时间复杂度是，

欢迎大家来到IT世界,在知识的湖畔探索吧!class Solution { public static int fib(int n) { int F[][] = new int[][]{{1, 1}, {1, 0}}; if (n == 0) { return 0; } power(F, n - 1); return F[0][0]; } /* Helper function that multiplies 2 matrices F and M of size 2*2, and puts the multiplication result back to F[][] */ public static void multiply(int F[][], int M[][]) { int x = F[0][0] * M[0][0] + F[0][1] * M[1][0]; int y = F[0][0] * M[0][1] + F[0][1] * M[1][1]; int z = F[1][0] * M[0][0] + F[1][1] * M[1][0]; int w = F[1][0] * M[0][1] + F[1][1] * M[1][1]; F[0][0] = x; F[0][1] = y; F[1][0] = z; F[1][1] = w; } /* Helper function that calculates F[][] raise to the power n and puts the result in F[][] Note that this function is designed only for fib() and won't work as general power function */ public static void power(int F[][], int n) { int i; int M[][] = new int[][]{{1, 1}, {1, 0}}; // n - 1 times multiply the matrix to {{1,0},{0,1}} for (i = 2; i <= n; i++) { multiply(F, M); } } }

复杂度分析

时间复杂度：，在于计算矩阵的次幂。
空间复杂度：
。

算法六：矩阵快速幂(分治快速幂运算)

算法五的时间复杂度是，但可以降低到，因为可以使用分治算法加快幂运算，加速这里的求取。如下所示：

class Solution { public int fib(int n) { if (n < 2) { return n; } int[][] q = {{1, 1}, {1, 0}}; int[][] res = pow(q, n - 1); return res[0][0]; } public int[][] pow(int[][] a, int n) { int[][] ret = {{1, 0}, {0, 1}}; while (n > 0) { if ((n & 1) == 1) { ret = multiply(ret, a); } n >>= 1; a = multiply(a, a); } return ret; } public int[][] multiply(int[][] a, int[][] b) { int[][] c = new int[2][2]; for (int i = 0; i < 2; i++) { for (int j = 0; j < 2; j++) { c[i][j] = a[i][0] * b[0][j] + a[i][1] * b[1][j]; } } return c; } }

复杂度分析

时间复杂度：。
空间复杂度：
，如果认为函数栈也算空间的话。

算法七：斐波那契数新算法求解

这是另外一种求解斐波那契数的算法，证明如下：

1. 矩阵形式的通项

不妨令：，，，

证明：

采用数学归纳法进行证明，

1. 当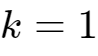时：

显然成立！

2. 当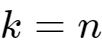时：

2. 偶数项和奇数项

因为，则有：

所以有：

3. 矩形形式求解Fib(n)

因为涉及到矩阵幂次，考虑到数的幂次的递归解法：

为奇数：

为偶数：

根据上述公式，我们可以写出如下代码：

欢迎大家来到IT世界,在知识的湖畔探索吧! public static int MAX = 1000; public static int f[]; // Returns n'th fibonacci number using // table f[] public static int fib(int n) { if (n == 0) { return 0; } if (n == 1 || n == 2) { return (f[n] = 1); } // If fib(n) is already computed if (f[n] != 0) { return f[n]; } int k = (n & 1) == 1 ? (n + 1) / 2 : n / 2; // Applying above formula [Note value n&1 is 1 if n is odd, else 0. f[n] = (n & 1) == 1 ? (fib(k) * fib(k) + fib(k - 1) * fib(k - 1)) : (2 * fib(k - 1) + fib(k)) * fib(k); return f[n]; }

复杂度分析

时间复杂度：。
空间复杂度：
。

算法八：通项公式(Using Formula)

斐波那契数是齐次线性递推，根据递推方程，可以写出这样的特征方程：

求得。

设通解为，代入初始条件，，得

，。

因此斐波那契数的通项公式如下：

得到通项公式之后，就可以通过公式直接求解第项。

class Solution { public int fib(int n) { double sqrt5 = Math.sqrt(5); double fibN = Math.pow((1 + sqrt5) / 2, n) - Math.pow((1 - sqrt5) / 2, n); return (int) Math.round(fibN / sqrt5); } }

复杂度分析

时间复杂度:
空间复杂度:

算法九：暴力法

如果不需要求解特别大的

欢迎大家来到IT世界,在知识的湖畔探索吧!class Solution { public: int fib(int n) { int nums[31]={0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368,75025,,,,,}; return nums[n]; } };

复杂度分析

时间复杂度:
空间复杂度:

总结

通过上述，我们使用了9种算法来求解斐波那契数列，这9种方法综合了递归、迭代、数学等各方面知识，值得认真学习！